Encontrando las zonas muertas de la red Wifi con una simple ecuación

Todos los que vivan en un apartamento de más de 40 metros cuadrados habrán notado en algún momento la atenuación de la señal de nuestro WiFi. Es una cuestión que depende de la distancia del dispositivo al router, el canal de frecuencia usado, los obstáculos y otros parámetros. Puede influir hasta la densidad del aire…

Después de lo que sabemos que pueden hacer las matemáticas no es sorprendente que os diga que existe una ecuación para hallar las zonas muertas de nuestro WiFi.

La clave la ha tenido Jason Cole, que ha sido el primero en resolver la ecuación de Helmholtz, que explica la propagación de las ondas electromagnéticas. Con ella, se permite aplicar las cuentas de forma matricial para simplificar el cálculo del camino tomado por las ondas y las interferencias que encuentra, y por consecuencia, su atenuación.

Jason Cole ha conseguido resolver la ecuación en dos dimensiones y aplicarla a su propio apartamento, a cuyas paredes les ha dado un gran coeficiente de refracción para considerarlas un buen obstáculo.

El experimento

WiFi-mapa

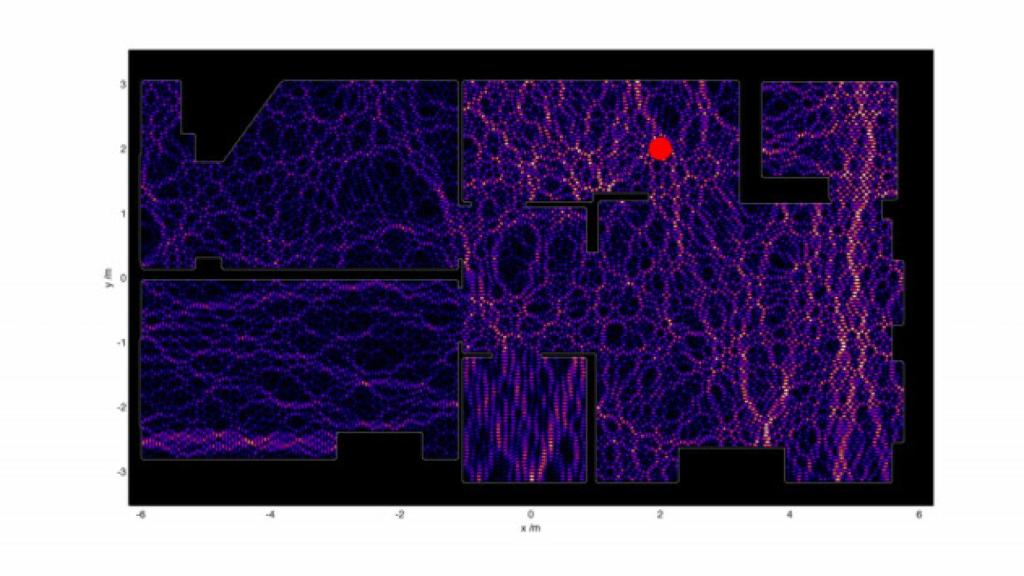
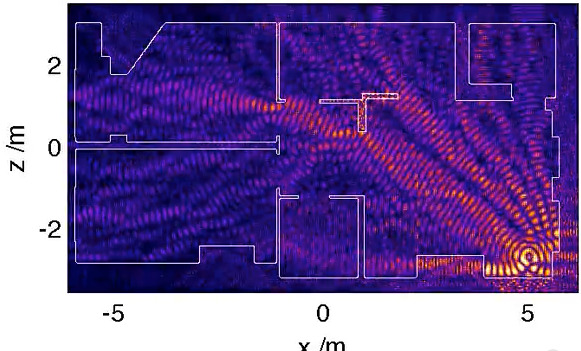
El resultado de su simulación fue bastante “lógico”, digamos. Al situar el router en el medio del apartamento obtenía buena cobertura en toda la superficie, aunque con varios “rizos” que podéis ver en la imagen causados por el choque con los obstáculos. Luego, al asignar un coeficiente de absorción de potencial mayor a los obstáculos, obtuvo una buena cobertura alrededor del router pero ligeras atenuaciones.

Más adelante añadió la variable del tiempo para poder dibujar un esquema de la evolución de las ondas electromagnéticas dentro de un intervalo de tiempo. Así pudo ver las oscilaciones de la actividad de las ondas, que en un tiempo era mayor o menor que en otros, y ver que como esperaba no era constante.

Como veis, la física y las matemáticas pueden aplicarse en cualquier campo de nuestras vidas, lo que quizás hace que lo entendamos un poco más… o menos.

Fuente | Ars Technica